Sé que tenéis miedo. Teméis los qubits. Teméis el cambio. Yo no conozco el futuro. No he venido para deciros cómo acabará todo esto. Al contrario, he venido a deciros cómo va a comenzar. Voy a terminar de escribir este artículo. Voy a enseñarles a todos lo que vosotros no queréis que vean. Les enseñaré un mundo sin vosotros. Un mundo sin bits y sin problemas de calor en los transistores, sin limites ni fronteras. Un mundo donde todos los estados sean posibles. Lo que hagáis después, es una decisión que dejo en vuestras manos.

En artículos anteriores (i y ii) ya introdujimos la computación cuántica, el Microsoft Quantum Development Kit, los qubits de forma básica y algo más avanzada, además de varias operaciones y puertas lógicas de este nuevo paradigma.
Y como lo prometido es deuda, hoy vamos a hablar de entrelazamiento y teleportación cuánticos:
Entrelazamiento
El entrelazamiento cuántico es algo más abstracto (si cabe ya) de explicar. Quizá lo más sencillo es verlo con un ejemplo:
Imaginad que tenemos dos qubits representados de la siguiente forma:
a|00> + b|01> + c|10> + d|11>
Donde: a y d valen uno partido de la raíz cuadrada de dos y b y c valen 0:
1/sqrt(2)|00> + 0|01> + 0|10> + 1/sqrt(2)|11> = (1/sqrt(2))(|00> + |11>)
Esto quiere decir que solo tenemos dos estados posibles con un 50% de posibilidades de que ocurra 00 o 50% de 11 mientras que no es posible que sea 01 ni 10.
Como ya vimos en otros artículos, en el momento en el que realizo una medida de un qubit este colapsa a ese estado. Una consecuencia del principio de incertidumbre.
Entonces si midiéramos el valor del primer qubit y este diera como resultado 0, esto significaría que el segundo qubit colapsaría también pasando a valer 0.
Podríamos decir que un estado de entrelazamiento es un estado en el que tener un valor en un qubit implica otro valor en otro qubit diferente.

A estos estados de entrelazamiento completo se les conoce como estados de Bell. Y para este ejemplo en concréto, se puede conseguir aplicando una fórmula con operaciones que ya hemos visto:
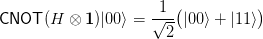
Esta misma formula escrita en Q# podría ser:
operation Entanglement(q1: Qubit, q2: Qubit): Unit
{
H(q1);
CNOT(q1, q2);
}
Donde aplicamos una puerta H al primer qubit y acto seguido una puerta CNOT usando como objetivo el segundo qubit. El resultado de estas dos operaciones es un estado de entrelazamiento semejante al usado en el ejemplo anterior: 50% 00 y 50% 11.
Ahora podríamos escribir el código de ejemplo de ejecución de la operación de entrelazar:
operation Set(q: Qubit, value: Result): Unit
{
let current = M(q);
if (current != value)
{
X(q);
}
}
operation MakeEntanglement(initial: Result): (Result, Result)
{
using (qubits = Qubit[2])
{
Set(qubits[0], initial);
Set(qubits[1], Zero);
Entanglement(qubits[0], qubits[1]);
let res0 = M(qubits[0]);
let res1 = M(qubits[1]);
ResetAll(qubits);
return (res0, res1);
}
}
Aquí simplemente asignamos un valor inicial a un par de qubits, realizamos el entrelazado y los medimos.
En C# podríamos realizar una prueba con este código:
using (var qsim = new QuantumSimulator())
{
var initials = new Result[] { Result.Zero, Result.One };
foreach (var initial in initials)
{
var res = MakeEntanglement.Run(qsim, initial).Result;
var (res1, res2) = res;
Console.WriteLine($"{res1} {res2}");
}
}
Que al ejecutar podría tener una salida semejante a:
$ dotnet run
Zero Zero
One One
Aunque podría tener diferentes combinaciones (por eso del 50% de posibilidades de uno y otro) siempre que se repitan el valor primero y segundo (por eso del entrelazamiento cuántico).
Teleportación
La teleportación cuántica es algo parecido a lo que piensas, pero no es exactamente como piensas.

La idea es conseguir enviar el estado de un qubit a a otro b que no se encuentra en el mismo lugar.
Para ello podemos usar el entrelazamiento cuántico como canal de comunicación:
Imaginemos que tenemos dos partículas entrelazadas como en el ejemplo anterior. Una la coges tu y la otra la cojo yo. Cada uno nos vamos a nuestra casa. En la comodidad del hogar decides mirar el valor de tu partícula, y en ese momento colapsas el valor de ambas. De forma que si la tuya vale 1 ya sabes que la mía vale 1.
Ahora, si tú copias el valor de otra partícula no entrelazada con la mía, en la que sí que está entrelazada, entonces podríamos decir que has pasado el estado de una tercera partícula hasta mi.
La realidad detrás de este experimento es que no se ha transmitido ninguna información. Esta información ya la teníamos tanto tú como yo. Y si yo llego a mirar primero el valor de mi partícula, hubiera obtenido el mismo resultado. Es lo que se conoce como la paradoja EPR, algo que escapa totalmente al ámbito de este artículo.
Podríamos aclarar (o complicar, no lo tengo claro) todo un poco más, usando un ejemplo con punteros de C++:
// esta es mi partícula
int mine = 1;
// esta es la tuya
int *yours = NULL;
// y este el valor que quieres teleportar
int other = 0;
// nos entrelazamos
yours = &mine;
// ahora cada uno nos iríamos a nuestra casa
// desde tu casa transformas el valor de tu partícula
*yours = other;
// el resultado final es que tanto tu partícula como la mia son 0
cout << "Mine: " << mine << endl;
cout << "Yours: " << *yours << endl;
Realizar esta operación en Q# es algo más complejo, pero no mucho. Si echamos un vistazo a la página de la wikipedia sobre el tema, nos propone unos pasos:
- Puerta CNOT
- Operador de Hadamard
- Medida y transmisión
- Finalmente se debería aplicar un operador
ZoXen el valor del qubitb, en dependencia de los valores medidos, para tener el valor original:
- Finalmente se debería aplicar un operador
operation Teleport (source : Qubit, target : Qubit) : Unit
{
// creamos un canal de transmisión
using (channel = Qubit())
{
// lo entrelazamos con el qubit objetivo
Entanglement(channel, target);
// puerta CNOT
CNOT(source, channel);
// operador de Hadamard
H(source);
// medida
let data1 = M(source);
let data2 = M(channel);
// transformación
if (data1 == One) { Z(target); }
if (data2 == One) { X(target); }
// dejar los qubits a Zero
Reset(channel);
}
}
Para llamar a la teleportación usaríamos la siguiente operación de Q#:
operation MakeTeleport(message : Result) : Result
{
using ((source, target) = (Qubit(), Qubit()))
{
Set(source, message);
Teleport(source, target);
let measurement = M(target);
ResetAll([source, target]);
return measurement;
}
}
Donde creamos dos qubits. En el primero guardamos el valor del mensaje que queremos enviar. Realizamos la teleportación y devolvemos el valor del destino.
El código en C# para probarlo sería algo como esto:
using (var qsim = new QuantumSimulator())
{
var initials = new Result[] { Result.Zero, Result.One };
foreach (var initial in initials)
{
var res = MakeTeleport.Run(qsim, initial).Result;
Console.WriteLine($"{initial} = {res}");
}
}
Y la salida que obtendríamos al ejecutar vendría a confirmar que se ha transmitido la información:
$ dotnet run
Zero = Zero
One = One

Como curiosidad, unos científicos chinos tienen el record de distancia de teleportación cuántica, llegando a 1200km de separación entre dos partículas entrelazadas ¡Ahí es nada!
Conclusiones
Creo que con esta tercera parte he conseguido resarcirme del fiasco de la anterior. Aquí se aplican prácticamente todos los conceptos que hemos ido explicando en los artículos anteriores y es cuando empezamos a ver dos capacidades muy potentes de la programación cuántica.
Por ejemplo, el uso de estas técnicas es fundamental en la criptografía cuántica: un tipo de encriptación de información mucho más seguro de los usados hoy en día. Y por extensión sería muy interesante el uso de ambas técnicas para conseguir una comunicación muy rápida y segura.

Eso sí, todo esto que comentamos, hoy en día, sería muy difícil de aplicar en el mundo real…
No te digo nada y te lo digo todo. Así a la vez.